How To Draw A Bode Plot With Complex Poles
Rules for Constructing Bode Diagrams
This certificate will discuss how to really draw Bode diagrams. It consists mostly of examples.
ane. Rewrite the transfer function in proper form.
A transfer function is commonly of the grade:

Equally discussed in the previous document, we would similar to rewrite this so the lowest order term in the numerator and denominator are both unity.
Some examples will clarify:
Case 1

Annotation that the concluding result has the lowest (zero) order power of numerator and denominator polynomial equal to unity.
Example 2

Note that in this example, the lowest power in the numerator was ane.
Example iii
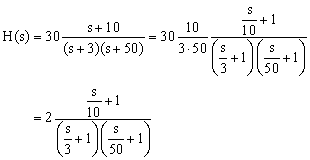
In this case the denominator was already factored. In cases like this, each factored term needs to accept unity as the lowest order power of s (aught in this case).
2. Separate the transfer role into its constituent parts.
The next step is to separate the function into its elective parts. There are vii types of parts:
- A abiding
- Poles at the origin
- Zeros at the origin
- Real Poles
- Real Zeros
- Complex conjugate poles
- Complex cohabit zeros
We can use the examples in a higher place to demonstrate once more.
Instance one

This function has
- a abiding of 6,
- a zero at southward=-10,
- and complex cohabit poles at the roots of s2+3s+50.
The circuitous conjugate poles are at due south=-1.5 ± j6.9 (where j=sqrt(-i)). A more common (and useful for our purposes) way to express this is to use the standard notation for a second club polynomial

In this case

Example 2

This function has
- a constant of 3,
- a zippo at the origin,
- and complex conjugate poles at the roots of southtwo+3s+50, in other words

Case 3
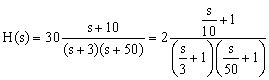
This function has
- a constant of 2,
- a zero at s=-x, and
- poles at due south=-3 and southward=-fifty.
3. Draw the Bode diagram for each part.
The rules for drawing the Bode diagram for each role are summarized on a separate folio. Examples of each are given afterward.
4. Describe the overall Bode diagram by adding up the results from step 3.
After the individual terms are drawn, information technology is a elementary affair to add them together. See examples, below.
Examples: Draw Bode Diagrams for the following transfer functions
These examples are compiled on the next page.
Instance 4
Repeated poles, a zero at the origin, and a negative constant
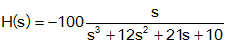
Full Solution
References
Replace
Source: https://lpsa.swarthmore.edu/Bode/BodeRules.html
Posted by: smithspoe1957.blogspot.com


0 Response to "How To Draw A Bode Plot With Complex Poles"
Post a Comment